为什么是"大"模型，而不是"小"而"精"的模型？ 能理解到人工神经网络是“函数近似器”，就能回答了—— 

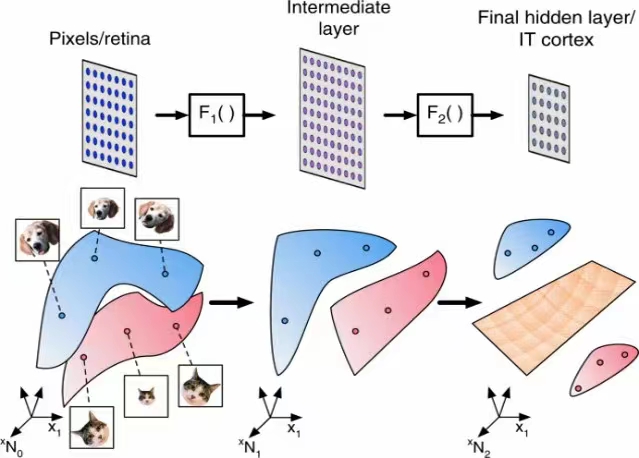
附图对人工神经网络的阐述，是我见过最简单，但追溯最久远的一个解释。说，人工神经网络的老祖宗，其实是线性回归，说白了就是一个一元一次函数，输出等于输入乘以一个系数，加上一个数值。我们今天看这个就是小学基础知识，可当年，这可是大名鼎鼎的“数学王子”高斯搞出来用来预测谷神星轨迹的，这奠定了直到今天还不少应用的"用一条直线整体逼近/穿过尽可能多的已知数据点，从而找到一个方程用来预测未知的数据点"的线性回归思想。

当然，高斯这种级别的天才自然觉得这也就是小儿科，连发表都懒得发表。但重点是他这个一元一次方程对预测天体运动轨迹很有效，引起了大家的注意。很快大家就发现，现实里描述一个事物规律的数据点，很多时候并不是直线，而可能是各种曲线；一个复杂表征，也不只有一维特征（一个变量），而是可能需要几十几百甚至成千上万维的变量，于是大家开始尝试增加更多元的变量，用很多直线组合出曲线，用组合出的曲线再表述出更复杂的曲线。这样复杂的曲线，就能够涵盖有模式但非常多维度的，非线性分布的数据点，这就有了神经元的雏形；直到今天，我们看任何再复杂的人工神经网络里的神经元，也就是另外一些神经元的线性组合，说明极复杂的概念表征（比如语言），也都能分解为变量的线性运算。这也是为什么深度学习里，最重要的一门基础课，就是线性代数。人工神经网络，也就成为了用来“拟合”任何一种函数 —— 从数字、文字，图像，声音等输入，到归类、判断、分析、生成的输出的映射 —— 的工具。

这种思想其实在科学发展中反复出现，从极限，微积分，到后来奠定计算机科学大厦逻辑地基的布尔代数（证明了任何复杂运算，都可以用几个最简单的“真”，“假”，“与”，“或”，“非”的逻辑运算实现），到傅里叶变换（任何周期函数都能用正弦余弦函数组合出来），分子生物/物理学，都遵循一个理念:不论多么复杂的事物，只要能一直分解下去，总是能分解为极为简单的元素组合。这甚至跟中国的“道生一，一生二，二生三，三生万物”的哲学理念不谋而合。

说到今天的“大模型”，为什么一定要“大”模型，而不是“小”而“精”的模型？我看了很多解释，都不是太满意。而从“回归”的数据点“fitting”的角度看，因为一个复杂事物的规律/特征/模式，是需要大量的多维数据“点”去描述的，比如说人类的文字系统，一个词，GPT-4的word embedding模型text-embedding-ada-002用了1536个维度去描述，假设总共有8万个词，那就意味着，有8万个具有1000多元（维）变量的数据点，根据词义/语法分布在1000多维的语义空间里，要真正理解这些词和词组合出来的句子，就需要大语言模型去“fitting”这些数据点；如果这个语言模型的参数不够大 —— 也就是数字神经元的连接不够 —— 也就是前面说的，能组合出“曲线”的线性组合太少，那不论如何调整这些不够多的参数值（也就是调整那个横穿1000多维空间的曲线的“形状”），都是凑不上 穿过/整体逼近这么多的数据点的。—— 仅代表尹智个人观点 Ken’s personal view only